In this article, we’ll be solving the given expression “x*x*x is equal to 2023‘ with the help of mathematical tools. This expression is basically in the cubic form, which means it holds the power 3.
This expression is a prime example of Algebra. In simple words, we can say that it is an Algebraic expression. Algebra is one of the universe from the cosmos of mathematics. It is one of the most complex topics that students talk about. The masters of Algebra are still studying it as it is never ending.
The given expression x*x*x is equal to 2023 or equation can be written as (x3) = 2023. We’ll be covering few things like, What is Algebra? How to solve this equation? What is square root method and more.
Mathematics is the favourite subject of everyone. Agree to Disagree ? In this article, we’ll be solving the equation to check whether the given term is right or not.
About Algebra Algorithm
Algebraic expression uses variables in mathematics. It uses the forms of letter and symbols to enact numerical forms. The given equation x*x*x is equal to 2023 doesn’t symbolise the year 2023, it’s just a numeric data. It Is used to define the relationship between the equation. It is an expression in which letters and symbols are applied to represent the numerical. It is used to check, whether the given equation is correct or not.
How to Calculate the term x*x*x is equal to 2023?
1. Simplification
We’ll be first converting or bringing the equation to its simplest form.
The given expression can be written in the form of (x3) = 2023.
2. Applying cubic root
To solve the equation, we need to apply cube root method. In this method, we apply cube root on both sides to remove the power. By taking the cube root on both sides, we can isolate the term ‘x’.
3. Isolation
The term isolation in mathematics means the rearrangement of the value of terms. By isolating the algebraic equation we can allow the variables to be on its own. Isolation is used to simplify the equation for easy and effective calculation.
- x = ∛2023
The term sqrt (3) is used to represent the presence of cube root on the value 2023.
Calculating the cube root of 2023 is not simple so, we’ll be doing the calculation on the calculator. Such concepts are easy to crack when we apply the accurate formula.
After calculating the values, we need to ensure that the outcome must be in the form or real number. The number when multiplied three times should generate the value comprehensive to 2023.
After Further calculation:
- x = ∛2023 = 12.647
- We found the value of term ‘x’ which is approximately 12.647
When we multiple the value of x by power 3 or multiplying the value 12.647 by 3 we get the final value of x3.
- [ x3 = 12.647 * 12.647 * 12.647 ]
- The value of x3 after the calculation is 2022.844
Prove the equation, x*x*x* = 2023
To prove that the following equation has a relationship, we need to apply mathematical tools in this equation.
- x*x*x* = 2023
- (x3) = 2023
Applying cube root on both sides to remove the power 3 from x.
- 3√(x)3= 3√2023
The cube root on the left hand side will get cancelled with each other.
We get;
- x = 3√ 2023
- x = 12.647
When we apply the value of the term ‘x’ in the given equation, we get:
- X3 = 2023
- 12.647 * 12.647 * 12.647 = 2023
After multiplication we get;
- Answer = [2022.84 ≈ 2023].
We get the final value of x3 as 2022.84 which is approximately equal to 2023. We can easily conclude that the given expression is correct in nature. The outcome is comprehensive to 2023.
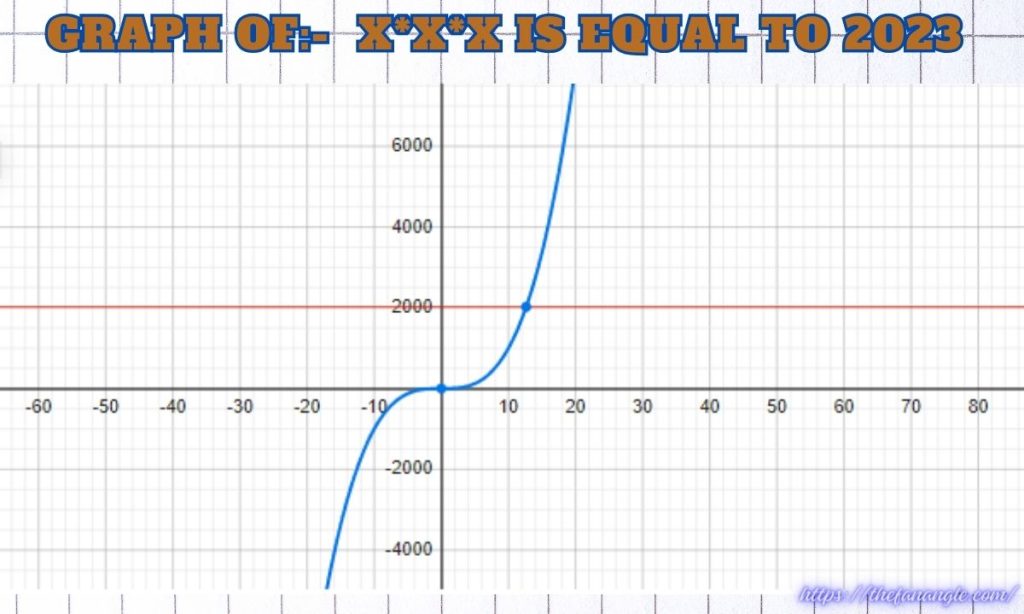
Graphical Representation of Given Equation x*x*x* = 2023
Advantages of Algebraic Calculation
- It is used to check whether the given equation is correct or not.
- It helps to solve the equation into the simplest form.
- To do unrealistic calculation, we need Algebra.
- Algebra is used to solve the complexity of mathematics.
- It is used to emphasise the relationship between the term.
Can we solved the equation [ x*x*x* = 2023 ] by factorisation method?
No, we can solve the equation by factorisation method. As we know that the value 2023 is not a perfect cube, we can’t apply the factorisation method. The outcomes will holds decimals doesn’t symbolises the perfect square root.
To solve any equation we need to have a perfect square or cube. There are various types of equations, all the equations can’t be solved by the same formula.
Where we can apply the term x*x*x is equal to 2023
- It is applied in the scenario of physics, mathematics, engineering and economics.
- With the help of such equation we can bring the out the relationship between the volume and the linear dimensions.
- It is even used in the geometric universe of mathematics.
- This kind of algebraic equations are used to solve the realistic world problems. From the calculation of the paint required to paint a walk to general physics and more.
- It is being applied in the real physical world, it might includes are regular work too.
Instruments used in the calculation
We have applied three applications of mathematics for the calculation of the term x*x*x is equal to 2023
- Cube root: After applying the simplification, we need to perform the isolation. To isolate the term x we need to apply cube root on both the sides of the equation.
- Round – Off: As 2023, is the not perfect cube number therefore, we need to do the round off. By comprehending the value we can prove that the given term was correct in nature.
- Simplification:- In this methods we break down the complexity of the equation. We convert the equation into simple form for easy calculation.
Conclusion
To check whether the term x*x*x is equal to 2023 is correct or not, algebra is applied. To calculate the answer for the term, we have used simplification, cube root application and rounding off the approximate term.
We have provided the conclusion by taking the approximate value. The above given term is correct or accurate in nature. The given term satisfies the principle of L.H.S = R.H.S
To solve such similar equations, we need to apply the same steps to calculate the outcome. The term is an example of Algebraic expression. This expression is used to solve simplest to complex algebraic problems and equations.
Also, Read About:-
