We have 2X2-3x- 5 = 0 as the given equation. Lets solve the equation by using the quadratic formula and other methods as well as.
Q. Equation :- 2X2-3x- 5 = 0
The equation at step’s conclusion is (2x2 – 3x) – 5 = 0.
Solution of 2X2-3x- 5 = 0:-
Dividing the middle word in an attempt to factor
- Multiplying 2 by 3 by 5
- The first term, 2x2, has a coefficient of 2.
- The coefficient of the middle word, -3x, is -3.
- “The constant” is the final term; it is -5.
Step 1: Use the constant 2 • -5 = -10 to double the first term’s coefficient.
Step 2: Locate two factors of -10 such that the sum of them equals the middle term’s coefficient, which is -3.-10 + 1 corresponds to 9 in addition to 5 in addition to 2 equals 3. That’s all.
Step 3: Utilize the two factor -5 and 2 found in step 2 above to rewrite the polynomial splitting the middle term.
- 2x2 – 5x + 2x – 5
Step 4: Sum up the first two terms and separate Common elements or variables.
- x • (2x–5)
Add the last two terms together and identify any commonalities:
- 1. • (2x–5)
Add the four phrases from step 4 together in step 5.
Which is the desired factorization, (x+1) • (2x-5)
Hence, we get (x+1) • (2x-5) =0 at end from 2×2-3x- 5 = 0.
Step 5:- Theory: A product’s foundation
- Multiple terms multiplied together equal zero.
- At least one of the terms must be 0 when the product of two or more terms equals zero.
- Now, we will solve each term = 0 independently.
- To put it another way, we will solve the same number of equations as there are terms in the final product.
- Any term = 0 solution also solves product = 0.
- Handling an Equation with Just One Variable:
- Work out 2x-5 equals 0.
- Add 5 on the both sides:
- 2x equals 5.
- Divide the equation’s two sides by two:
- x is equal to 5/2, or 2.500.
- x= 5/2
- Fixing an Equation with Just One Variable:
- Find the solution to x+1 = 0.
- Take one away from either side of the equation:
- x = -1
- Supplement: Direct Solution of Quadratic Equation Direct solution of 2×2-3x- 5 = 0.
Hence, at the end we get x= 5/2 and x = -1
This polynomial was previously factored by separating the middle term. Now let’s use the Quadratic Formula and Complete the Square to solve the equation.
Another Solution of 2X2-3x- 5 = 0 using Quadratic formula
The Quadratic formula is x=(−b±√b2−4ac)/2a.
From Above we can can
- 2x2, has a coefficient of 2
- -3x, is -3
- The constant is -5
Now, Add these values into the Quadratic formula
- x=[−(−3)±√(−3)2−4(2)(−5)]/2(2)
- x=(3±√9+40)/4
- x=(3±√49)/4
- x=(3±7)/4
- x=10/4 and −4/4
- Hence, x=52 and −1
Graph of 2X2-3x- 5 = 0:-
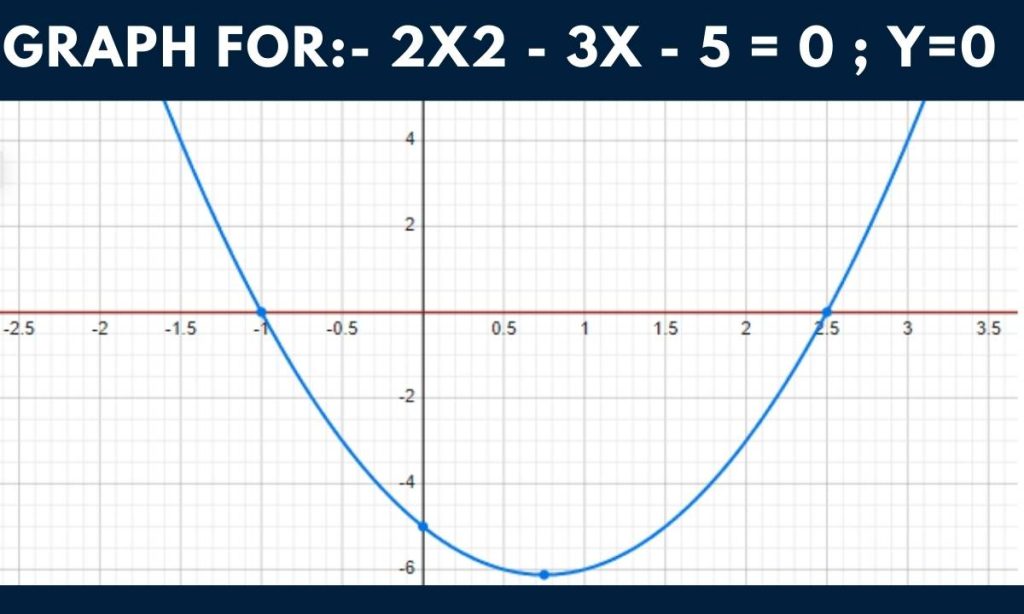
Parabola, Vertex Finding: Locate the Vertex of y = 2x2-3x-5
A parabola’s vertex is its highest or lowest point. As a result of opening up, our parabola has an absolute minimum or lowest point. The fact that the first term’s coefficient, 2, is positive (larger than zero), allows us to know this even before we plot “y”.
A vertical line of symmetry travels across the vertex of every parabola. Due to its symmetry, the line of symmetry would, for instance, cross the middle of the parabola’s two x-intercepts, which are its roots or solutions. That is, assuming there are two actual solutions to the parabola.
Many real-world scenarios, such as the height above the ground of an object thrown upward after a certain amount of time, can be modeled using parabolas. We can get information from the parabola’s vertex, such as the highest point an object thrown upwards can go. We therefore need to be able to determine the vertex’s coordinates.
- -B/(2A) gives the x-coordinate of the vertex for any parabola, Ax2+Bx+C. The x coordinate in our instance is 0.7500.
- By entering 0.7500 for x in the parabola formula, we can determine the y-coordinate:
- 3.0 * 0.75 – 5.0 = 2.0 * 0.75 * 0.75
- or y = -6.125
The root plot for the following equation represents the parabola:
y = 2X2-3x- 5 Axis of Symmetry (dashed) {x} = { 0.75}
- \x,y} = {0.75,-6.12} is the vertex.
- x-Intercepts at the Roots:
- At {x,y} = {-1.00, 0.00}, root 1
- At {x,y} = { 2.50, 0.00}, root 2
The Quadratic Equation can be solved by Completing the Square (4.2). This will solve the equation 2X2-3x- 5 = 0.
To find the coefficient of the first term, divide both sides of the equation by 2: x2-(3/2)x-(5/2) = 0
To both sides of the equation, add 5/2:
- x2-(3/2)x equals 5/2.
Here’s the cunning part: After taking the coefficient of x, which is 3/2, dividing it by two to get 3/4, and then square it to get 9/16
To both sides of the equation, add 9/16:
Located on the right-hand side is:
- 5/2 plus 9/16
The two fractions’ common denominator is 16. 49/16 is obtained by adding (40/16) and (9/16).
So when we add to both sides, we at last obtain:
- 9/16 + x2-(3/2) = 49/16
The left-hand side has been finished into a perfect square by adding 9/16:
The equation will be stated as above
According to the square root criteria, two items have equating square roots when they are equal side.
The square root of (x-(3/4)) is note full.2 is equal to (x-(3/4))2/2 equals (x-(3/4))1 is equates to x-(3/4)
Now, use above 2X2-3x- 5 = 0 equation and the Square Root Principle, we get: x-(3/4) = √ 49/16
- To get: Add 3/4 to each side.
- x is equal to 3/4 + √ 49/16.
Given this a square root has two value: a positive and a negative value.
- x2 – (3/2)There are two solutions to x – (5/2) = 0:
- Wheather x = 3/4 – √ 49/16 or x = 3/4 + √ 49/16
It can be noted that √ 49/16 can be stated as √ 49 / √ 16, or 7 / 4. Use the formula 4.3 to solve the quadratic equation 2X2-3x- 5 = 0.
The answer to the equation Ax2+Bx+C = 0, where A, B, and C are alphabets—often stated to as coefficients—is provided by the quadratic formula, x.
- The formula for x is B ± − B2-4AC.
- In our scenario, A = 2 B = -3 C = -5
- Thus, B2 – 4AC = 9 – (-40) = 49
Making use of the quadratic formula in 2X2-3x- 5 = 0
- Three plus fifty-nine is equal to x.
- Can √ 49 be made simpler?
- Indeed! 7•7 is the prime factorization of 49.
As we are taking a square, or second root, anything that we want to remove from under the radical must exist in two instances.
Thus, we are now examining:
- ( 3 ± 7) / 4 is the value of x.
Two practical answers:
- x equals (3+√49)/4, (3+7)/4, and 2.5
- x = (3-69)/4 = (3-6-7)/4 = -1.000
Also, Read About:-
